While the natal Moon and planets define your unique TIME period of birth, the AC(Ascendant) and MC are more concerned with the
SPACE you occupy on this Earth plane and are the foundational elements of true astrology. Note: For some odd reason I have chosen to
rename the Ascendant abbreviation as AC rather than Asc. Just my personal touch on it.
Yes, while the AC and MC also deal with time within the context of a 24-hour day, their special significance is that they map you out
locally on the Earth plane, like two crosshairs in a guidescope. The AC lines or signs(here in yellow) run across the astro map in a more or
less diagonal fashion, while the MC lines or signs(here in red) are perfectly vertical. The exceptions are at the equinoxes(0 Aries and 0 Libra
points) where both the AC and MC lines meet and are perfectly vertical.(see diagram below)
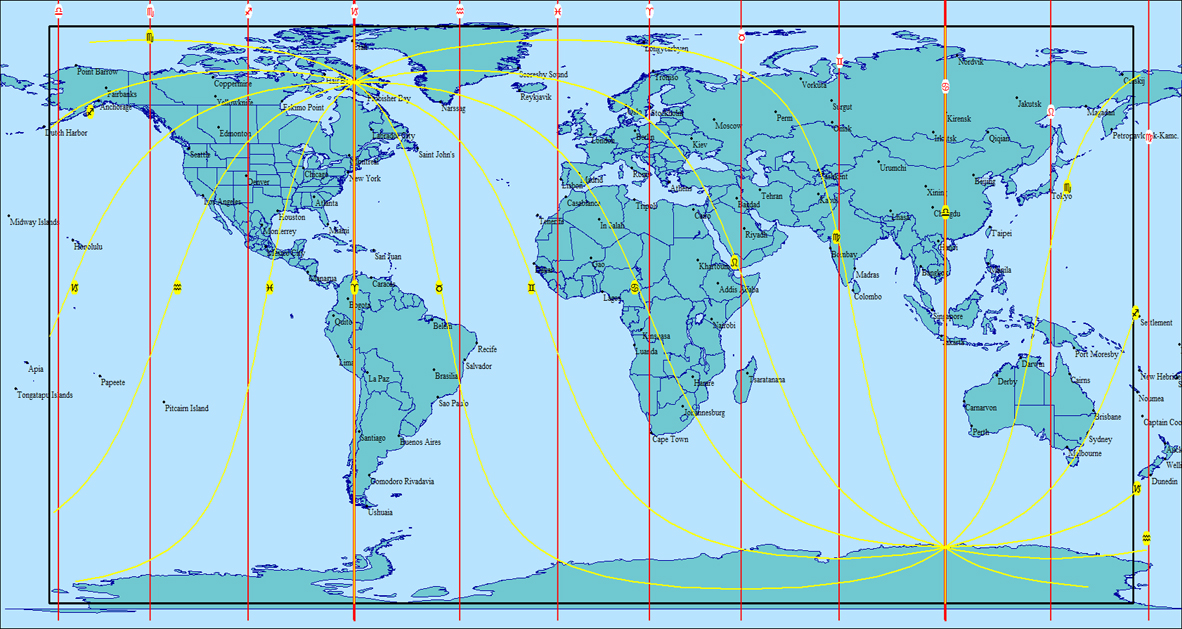 Where the 1st(AC) and 10th(MC) intersect is where your birth space is(see image below) and the qualities of this space, both cultural and astrological are what will define you most personally. In the example below, the native has Cancer rising or Ascendant with a Pisces MC(whole signs/houses are used here). While the native will connect with the entirety of the AC and MC spaces, where the two meet or merge(shaded area) is particularly potent, as are any planets running through it. The countries or regions here are of special signficance to the native. He or she will absorb the cultural and astrologuical influences here most readily and they will become the foundation of his or her being. The exact birth place(where the exact AC and MC degree lines merge), in this case Rouen, France, will of course be the central emanating point for the shaded area. 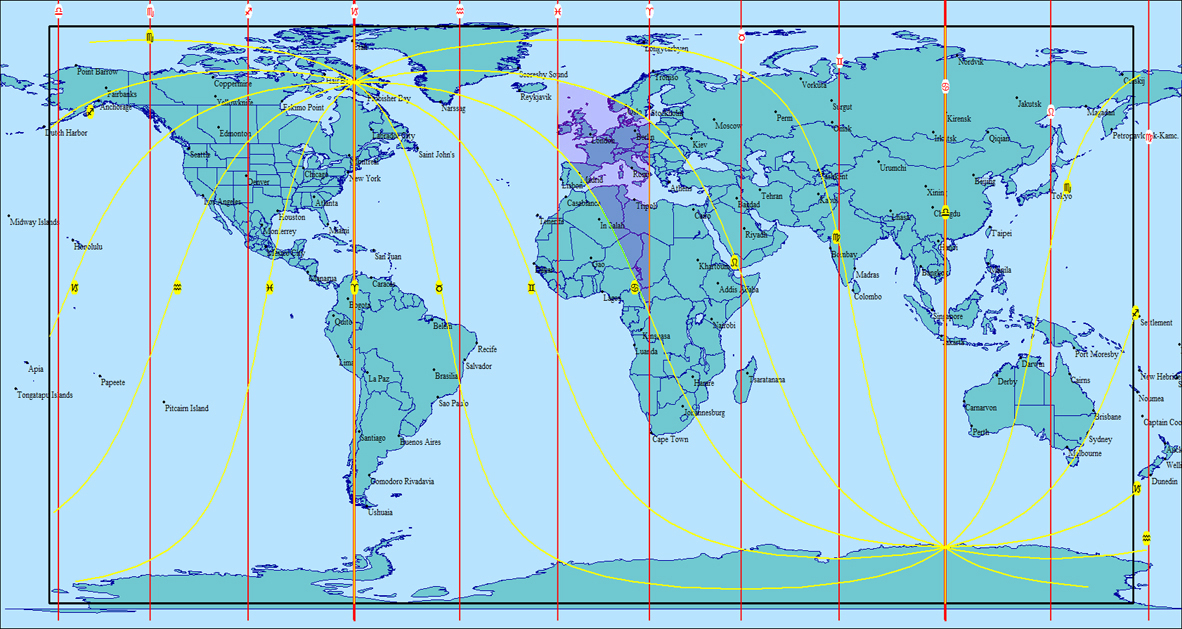 In my own case, being born in south-central Italy, I have south-central Europe as well as much of north-central Africa as my personal local space. This in large part explains my ease or similarity with the natives of this region, both mentally and culturally. Even here in Canada, I am more comfortable or in sync with the immigrants coming from those areas. I have also noted that the general latitude of your birthplace is also an important consideration for synchronizing or relating to others on a similar levels no matter what part of the Earth, although other astrological factors can mitigate this. The Moon, as the closest and fastest moving planet(2.25 days per sign average), serves as a kind of bridge between the "angles"(AC, MC, and their opposite points, IC and DC) and the planets, but there is still a wide gap here so that it remains extraneous to the Earth(AC) and Sky(MC) planes. There is talk in esoteric circles of a closer object to the Earth than the Moon having a weekly rather than monthly orbit, but it is etheric in nature and therefore invisible to human sight. If such an object does exist it would strengthen the link between the Earth and the Heavens. To know which part of the Earth(and Heaven) you are rooted in(besides your native country) you must know your exact time of birth which will yield your AC and MC positions. Without this information you have only the unhoused planets to define you, and sometimes not even some of these -if they are on the verge of changing signs. When the AC and MC are known, not only are your planets housed or rooted, but your own particular space or region on this Earth plane and how it influences you becomes better defined.
|